A camera model is a mathematical modelization of the mapping from world coordinates to image coordinates. This transformation process is fundamental to how cameras capture a three-dimensional scene and translate it into a two-dimensional image.
This modelization is essential for various applications, including stereo camera systems, driver monitoring systems (DMS), and image dewarping, among others.
The mapping from a three-dimensional point to a pixel can be separated into two phases, involving both extrinsic and intrinsic parameters. These two types of parameters work together to accurately depict how a camera captures an image from the world around it.
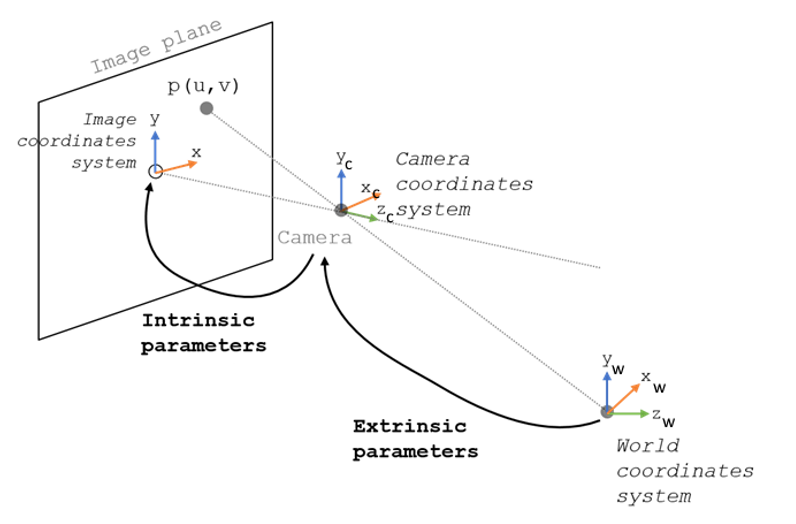
Extrinsic Parameters
Extrinsic parameters describe the position and orientation of the camera relative to the world coordinate system.
To convert world coordinates to camera coordinates, we use both the rotation matrix and the translation vector that constitute the extrinsic parameters of the camera. The typical form of the transformation matrix used to describe this conversion is a 4×4 matrix in homogeneous coordinates. This matrix is structured as follows:
1. Rotation (R): A 3×3 matrix that describes the camera’s orientation relative to the world coordinate system.
2. Translation (t): A 3×1 vector that represents the position of the camera’s origin in the world coordinate system.
The complete extrinsic parameter matrix \( \mathbf{E} \) can be expressed as:
\[\begin{bmatrix}x_c \\y_c \\z_c \\1\end{bmatrix}= \begin{bmatrix}R_{11} & R_{12} & R_{13} & t_x \\R_{21} & R_{22} & R_{23} & t_y \\R_{31} & R_{32} & R_{33} & t_z \\0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x_w \\y_w \\z_w \\1\end{bmatrix}\]
Where \( (x_w, y_w, z_w) \) are the coordinates of a point in the world coordinate system, and \( (x_c, y_c, z_c) \) are the coordinates of the same point in the camera coordinate system.
Here, the components \( R_{ij} \) are the elements of the rotation matrix \( \mathbf{R} \), and \( t_{x} \), \( t_{y} \), \( t_{z} \) are the components of the translation vector \( \mathbf{t} \). This matrix serves the following purposes:
– Rotation: Adjusts the orientation of the world coordinates to align with the camera’s coordinate system.
– Translation: Shifts the origin of the world coordinate system to the camera’s position.
Intrinsic Parameters
Intrinsic parameters describe the camera’s internal characteristics that affect the image formation process without reference to the scene being observed.
Absolutely, here’s how you might structure and begin the detailed discussion of various camera models focusing on their intrinsic parameters:
Camera Models for Intrinsic Parameters
In this section, I will present four different camera models, each characterized by how they handle intrinsic parameters. We begin with the simplest and most foundational model, the pinhole camera model.
1. Pinhole Camera Model
The pinhole camera model is the most basic yet essential model in the field of photogrammetry and computer vision. It represents an ideal camera that captures images without lens distortions.
Description:
– Concept: In the pinhole camera model, light passes through a single point (the pinhole) before reaching the image sensor. This simplicity results in images with no optical distortions, thereby providing a pure geometric representation of the scene.
– Camera Matrix: The intrinsic matrix for a pinhole camera is straightforward, involving only the focal length and the principal point, with the skew typically set to zero.
Mathematical Formulation:
– The intrinsic parameters in the pinhole model are encapsulated in the camera matrix, \( \mathbf{K} \), defined as:
\[\mathbf{K} = \begin{bmatrix}f_x & 0 & c_x \\0 & f_y & c_y \\0 & 0 & 1 \end{bmatrix} \]
– Projection Equation: Points in the scene are projected onto the image plane using the equation:
\[ \begin{bmatrix}u \\v \\1\end{bmatrix} = \mathbf{K} \cdot \begin{bmatrix}X/Z \\Y/Z \\1\end{bmatrix}\]
Here, \( (X, Y, Z) \) are the coordinates of a point in the camera’s coordinate system, and \( (u, v) \) are the corresponding coordinates on the image sensor.
2. The Brown-Conrady Model
The Brown-Conrady model is an advanced camera model that extends the basic pinhole camera model by including parameters to correct for lens distortions. This model is particularly useful in high-accuracy applications where even minor distortions can significantly impact the outcome.
The Brown-Conrady model is designed to address both radial and tangential lens distortions that commonly affect cameras.
Key Components :
Radial Distortion: This is the primary type of distortion corrected by the Brown-Conrady model. It occurs when light rays bend more near the edges of the lens than at the center, causing images to bulge outwards or inwards. The model uses polynomial coefficients \( k_1, k_2, \ldots \) to model these effects, typically up to the second or fourth power.
Tangential Distortion: Caused by the lens and sensor not being perfectly parallel, tangential distortion makes the image appear to be tilted at an angle. This is corrected using parameters \( p_1 \) and \( p_2 \), which shift the image along the x and y axes to realign it.
Mathematical Representation:
In the Brown-Conrady model, the radial and tangential distortions are corrected using polynomial equations that adjust the x and y coordinates from the idealized (undistorted) positions:
Radial Distortion
Radial distortion is typically modeled with the following polynomial equation, where \(r\) is the radial distance from the center of the image (the principal point):
\[x_{\text{distorted}} = x_{\text{ideal}} \left(1 + k_1 r^2 + k_2 r^4 + k_3 r^6\right)\]\[y_{\text{distorted}} = y_{\text{ideal}} \left(1 + k_1 r^2 + k_2 r^4 + k_3 r^6\right)\]
Where:
– \(x_{\text{ideal}}\) and \(y_{\text{ideal}}\) are the coordinates computed by the pinhole camera model.
– \(k_1, k_2, k_3\) are the coefficients for radial distortion.
Tangential Distortion
Tangential distortion occurs due to misalignment of the lens elements and sensor plane, causing the image to skew. It’s corrected using:
\[x_{\text{distorted}} = x_{\text{ideal}} + 2p_1 xy + p_2(r^2 + 2x^2)\]\[y_{\text{distorted}} = y_{\text{ideal}} + p_1(r^2 + 2y^2) + 2p_2 xy\]
Where:
– \(p_1\) and \(p_2\) are the coefficients for tangential distortion.
– \(xy\) is the product of the x and y coordinates from the ideal image point.
Complete Distortion Correction:
The complete model for distortion correction combines these effects. The coordinates \(x\) and \(y\) in the image after applying both radial and tangential distortion corrections can be derived by combining the effects described above:
\[x_{\text{corrected}} = x_{\text{ideal}} \left(1 + k_1 r^2 + k_2 r^4 + k_3 r^6\right) + 2p_1 xy + p_2(r^2 + 2x^2)\]\[y_{\text{corrected}} = y_{\text{ideal}} \left(1 + k_1 r^2 + k_2 r^4 + k_3 r^6\right) + p_1(r^2 +2y^2) + 2p_2 xy\]
Conclusion:
The Brown-Conrady model is widely used in fields of computer vision. It is the default camera model used in OpenCV. However, this model is accurate for cameras with a FOV up to 90°. Therefore, we need to introduce a new model for fisheye lenses.
3. Kannala-Brandt Model
The Kannala-Brandt model is specifically designed to calibrate cameras equipped with wide-angle and fisheye lenses, which exhibit significant radial distortion. This model provides a more flexible and accurate approach for modeling the complex distortions inherent in these lenses, making it highly suitable for applications requiring a broad field of vision.
Key Components:
Radial Distortion: Unlike simpler models that may use a quadratic or quartic polynomial, the Kannala-Brandt model employs an even polynomial expansion to model radial distortions. It uses the following equation to describe how each image point is distorted radially:
\[\theta = \arctan\left(\frac{\sqrt{x^2 + y^2}}{f}\right)\]\[r(\theta) = k_1 \theta + k_2 \theta^3 + k_3 \theta^5 + k_4 \theta^7 + \ldots\]
Where:
– \( \theta \) is the angle of incidence of a light ray striking the lens.
– \( r(\theta) \) is the radial distance from the optical axis, calculated as a polynomial function of \( \theta \), with \( k_i \) representing the coefficients of the polynomial.
– \( f \) represents the focal length of the lens.
Angle of Incidence**: This model uniquely considers the angle at which light enters the lens, which is crucial for accurately modeling the distinctive “bulging” effect seen in fisheye lens images.
Mathematical Representation:
To compute the final image coordinates, \( (x_{\text{distorted}}, y_{\text{distorted}}) \), the Kannala-Brandt model applies the radial distortion function to the angle of incidence:
\[x_{\text{distorted}} = x \cdot \frac{r(\theta)}{\sqrt{x^2 + y^2}}\]\[y_{\text{distorted}} = y \cdot \frac{r(\theta)}{\sqrt{x^2 + y^2}}\]
These equations ensure that the radial distortion adjustment is proportional to the original distance from the optical axis, preserving the unique visual characteristics of fisheye and wide-angle lenses.
Conclusion:
By accurately addressing the radial distortions typical of fisheye and wide-angle lenses, the Kannala-Brandt model represents a robust solution for camera calibration in specialized applications.
4. Fisheye62 model
The Fisheye62 model is an enhancement of the KB3 model that incorporates tangential distortion, further refining the projection of points from the camera to the image plane. This model is particularly adept at correcting the distortive effects that are not addressed by radial distortion correction alone.
Tangential Distortion in the Fisheye62 Model
Tangential distortion occurs because the image-taking lens is not perfectly parallel to the imaging plane. To correct for this, the Fisheye62 model introduces two new coefficients, \( p_0 \) and \( p_1 \), which help adjust the image coordinates to account for the tangential distortion.
The projection function for the Fisheye62 model is given by:
\[u = f_x \cdot (u_r + t_x(u_r, v_r)) + c_x, \]\[v = f_y \cdot (v_r + t_y(u_r, v_r)) + c_y,\]
where:
– \( u_r = r(\theta) \cos(\phi) \),
– \( v_r = r(\theta) \sin(\phi) \).
\( u_r \) and \( v_r \) are the rectified image coordinates that would be obtained in the absence of tangential distortion.
The tangential distortion components, \( t_x \) and \( t_y \), are defined as:
\[t_x(u_r, v_r) = p_0(2u_r^2 + r(\theta)^2) + 2p_1u_rv_r,\]\[t_y(u_r, v_r) = p_1(2v_r^2 + r(\theta)^2) + 2p_0u_rv_r,\]
This allows the Fisheye62 model to adjust the image coordinates by shifting them to where they would be located if there were no tangential distortion.
Conclusion:
The Fisheye62 model is a powerful tool for correcting tangential distortions in images, particularly those captured with fisheye lenses that exhibit a high degree of distortion. By employing this model, practitioners in fields such as photogrammetry, computer vision, and robotics can significantly improve the accuracy of the inferred geometric information from their imaging systems.
5. FisheyeRadTanThinPrism model
The FisheyeRadTanThinPrism model, also known as Fisheye624, is an intricate camera model that accommodates thin-prism distortion on top of the already detailed Fisheye62 model. Its sophistication lies in its four additional coefficients: \( s_0, s_1, s_2, s_3 \), which address the thin-prism distortion, denoted as \( tp \).
Projection Function:
The model’s projection function is as follows:
\[\begin{align*}u &= f_x \cdot (u_r + t_{px}(u_r, v_r)) + c_x, \\v &= f_y \cdot (v_r + t_{py}(u_r, v_r)) + c_y.\end{align*}\]
Here, \( u_r \) and \( v_r \) are the undistorted coordinates in the radial model, and \( t_{px} \) and \( t_{py} \) are the adjustments for thin-prism distortion, enhancing the model’s precision in capturing the peculiarities of fisheye lens imagery.
Defining Thin-Prism Distortion:
The thin-prism distortions \( t_{px} \) and \( t_{py} \) are mathematically defined as:
\[\begin{align*}t_{px}(u_r, v_r) &= s_0r(\theta)^2 + s_1r(\theta)^4, \\t_{py}(u_r, v_r) &= s_2r(\theta)^2 + s_3r(\theta)^4,\end{align*}\]
with \( r(\theta) \) representing the radial distance as a function of the angle \( \theta \). These equations meticulously adjust for the light bending due to thin-prism effects that can cause image skewing and asymmetry.