How do we assess color accuracy between different images? Unfortunately, the commonly used RGB color space is not perceptually uniform, which means that equal changes in RGB values do not correspond to equal perceived changes in color. This inconsistency can lead to inaccuracies in color reproduction across various devices.
The Lab color space, on the other hand, is designed to be perceptually uniform. It separates lightness (L*) from color information (a* and b*), making it ideal for precise color manipulation and comparison. By converting images from RGB to Lab, we can measure color differences using Delta E (ΔE), ensuring consistent and accurate color reproduction in digital imaging workflows. Delta E quantifies the difference between two colors, allowing for objective assessment of color accuracy.
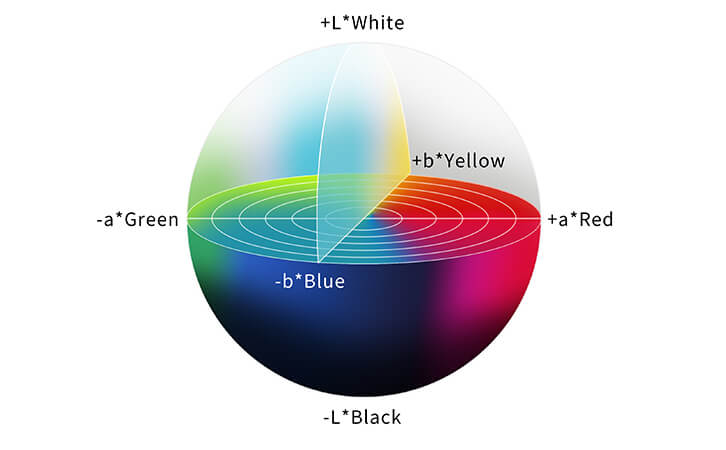
The Lab color space consists of three components:
1. L* (Lightness)**: Represents the lightness of the color, ranging from 0 (black) to 100 (white).
2. a* (Green-Red Axis)**: Represents the color position between green and red. Negative values indicate green, and positive values indicate red.
3. b* (Blue-Yellow Axis)**: Represents the color position between blue and yellow. Negative values indicate blue, and positive values indicate yellow.
Please see below for some graphical representations of this color space :
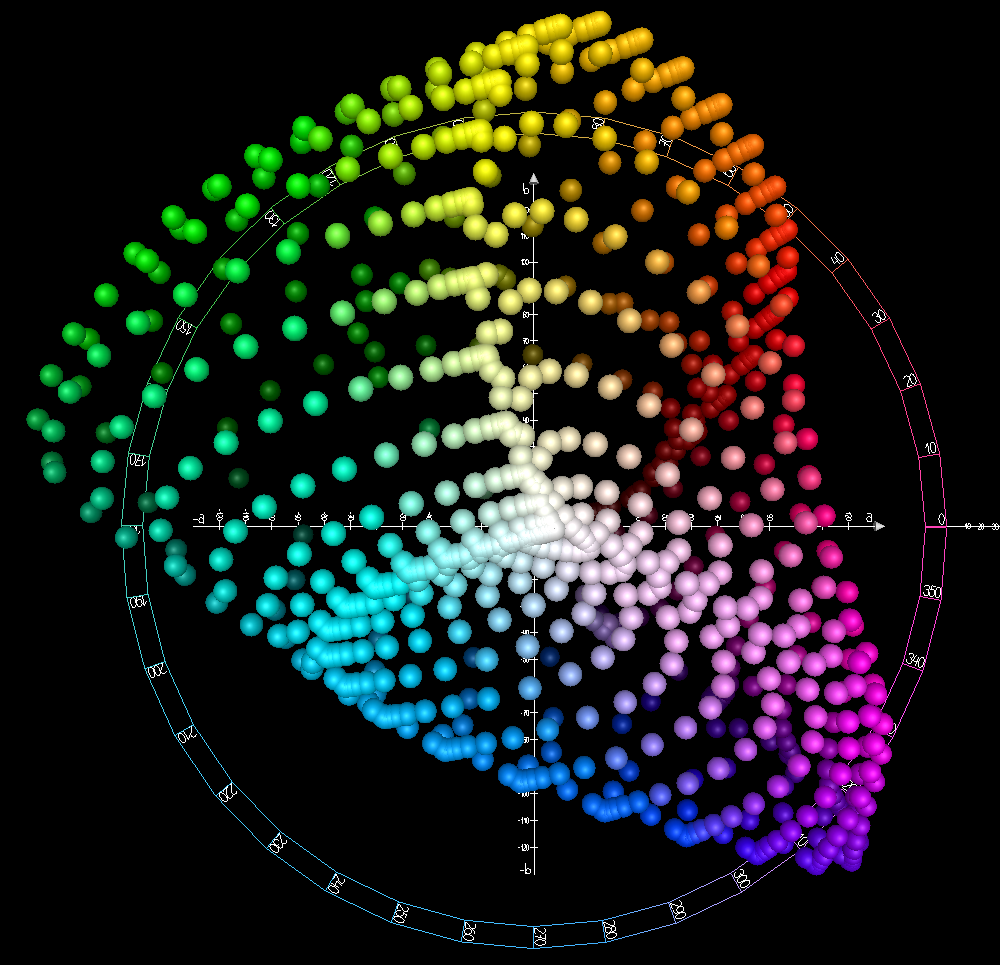
Ok great, now we have a perceptually uniform color space. But how do I convert the RGB color form an image taken with my camera to the Lab colors space ? Let’s find out :
How to Convert from sRGB to Lab Color Space?
Converting from sRGB to Lab color space involves several steps, including a transformation to an intermediate color space (XYZ). The best resource to get all the math for color conversion is the well-known Bruce Lindbloom website that every image quality engineer should know (http://brucelindbloom.com/index.html). But let me summarize it in the most common case:
1. Normalize the RGB Values
First, normalize the sRGB values (R, G, B) to the range [0, 1] by dividing each value by 255.
\[R’ = \frac{R}{255}\]
\[G’ = \frac{G}{255}\]
\[B’ = \frac{B}{255}\]
2. Apply Gamma Correction
Apply gamma correction to the normalized sRGB values to get linear RGB values.
\[R_{\text{linear}} = \begin{cases}\left(\frac{R’ + 0.055}{1.055}\right)^{2.4} & \text{if } R’ > 0.04045 \\\frac{R’}{12.92} & \text{otherwise}\end{cases}\]
\[G_{\text{linear}} = \begin{cases}\left(\frac{G’ + 0.055}{1.055}\right)^{2.4} & \text{if } G’ > 0.04045 \\\frac{G’}{12.92} & \text{otherwise}\end{cases}\]
\[B_{\text{linear}} = \begin{cases}\left(\frac{B’ + 0.055}{1.055}\right)^{2.4} & \text{if } B’ > 0.04045 \\\frac{B’}{12.92} & \text{otherwise}\end{cases}\]
3. Convert to XYZ Color Space
Use the linearized RGB values to calculate the corresponding XYZ values using the standard transformation matrix. The transformation matrix used here assumes a D65 reference white as expected with the sRGB color space.
\[\begin{pmatrix}X \\Y \\Z\end{pmatrix}=\begin{pmatrix}0.4124564 & 0.3575761 & 0.1804375 \\0.2126729 & 0.7151522 & 0.0721750 \\0.0193339 & 0.1191920 & 0.9503041\end{pmatrix}\begin{pmatrix}R_{\text{linear}} \\G_{\text{linear}} \\B_{\text{linear}}\end{pmatrix}\]
4. Convert to Lab Color Space
Convert the XYZ values to Lab using the following formulas. Note that we typically use the 2° standard observer for this conversion, as it is the most commonly used for color matching.\[X_n = 0.95047 \quad (\text{reference white point for D65 illuminant})\]\[Y_n = 1.00000\]\[Z_n = 1.08883\]\[f(t) = \begin{cases}t^{\frac{1}{3}} & \text{if } t > 0.008856 \\7.787 \cdot t + \frac{16}{116} & \text{otherwise}\end{cases}\]\[L^* = 116 \cdot f\left(\frac{Y}{Y_n}\right) – 16\]\[a^* = 500 \cdot \left( f\left(\frac{X}{X_n}\right) – f\left(\frac{Y}{Y_n}\right) \right)\]\[b^* = 200 \cdot \left( f\left(\frac{Y}{Y_n}\right) – f\left(\frac{Z}{Z_n}\right) \right)\]
Selecting the White Point
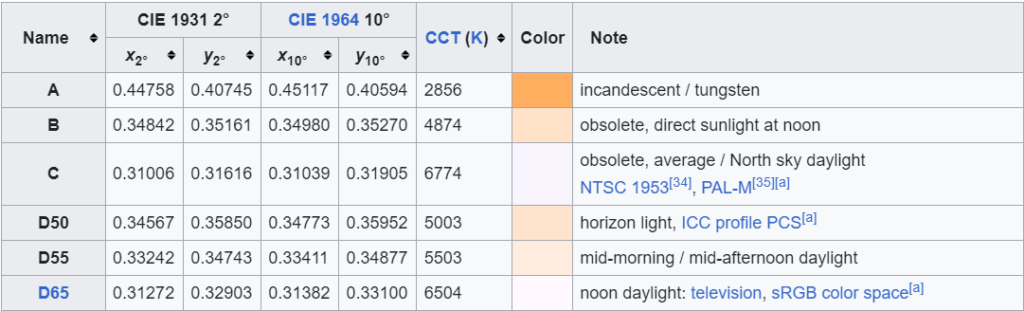
The white point is a reference point in color space that represents the color “white” under specific lighting conditions. The white point value also depends on the standard observer used (2° or 10°). The choice of white point is crucial as it affects the color appearance in the Lab color space. Different industries and applications may use different white points. Here are some common white points:
D65: This is the standard illuminant used for average daylight. It is commonly used in digital imaging and sRGB color space conversions. The reference values are:\[X_n = 0.95047, \quad Y_n = 1.00000, \quad Z_n = 1.08883\]Using the standard 2° observer, the CIE 1931 color space chromaticity coordinates of D65 are:\[x = 0.31272, \quad y = 0.3290 \]
and the corresponding XYZ tristimulus values are: \[X = 95.047, \quad Y = 100, \quad Z = 108.883\]
For the supplementary 10° observer, the coordinates are:\[x = 0.31382, \quad y = 0.33100 \]
and the corresponding XYZ tristimulus values are:\[X = 94.811, \quad Y = 100, \quad Z = 107.304\]
D50: This is often used in the printing industry and represents a warmer, more yellowish light than D65. The reference values are:\[X_n = 0.96422, \quad Y_n = 1.00000, \quad Z_n = 0.82521\]
E: This represents equal energy white light. It is less common but sometimes used for theoretical purposes. The reference values are:\[X_n = 1.00000, \quad Y_n = 1.00000, \quad Z_n = 1.00000\]
Choosing the correct white point depends on the specific application and the lighting conditions under which the colors will be viewed. For example, sRGB is defined relative to a D65 reference white, and ICC profiles are defined relative to a D50 reference white.
For lazy people like me, I recommend using the scikit-image library for any implementation in Python. The following line of code will convert any sRGB value into the Lab color space given the illuminant and standard observer:
skimage.color.rgb2lab(rgb, illuminant='D65', observer='2', *, channel_axis=-1)