In the last article (From RGB to L*a*b* color space), I presented how to convert a color in the RGB color space to the Lab one and explained that it is used to measure color accuracy. Measuring color accuracy is an important tool in various fields such as printing and, more importantly, digital imaging. Indeed, when taking a picture or a video, you want to ensure that the colors you see with your eyes are properly recorded. Also, in the computer vision field, you want to ensure color consistency between the training and evaluation datasets as well as for all the cameras you will build in serial production to guarantee performance.
COLOR CHART
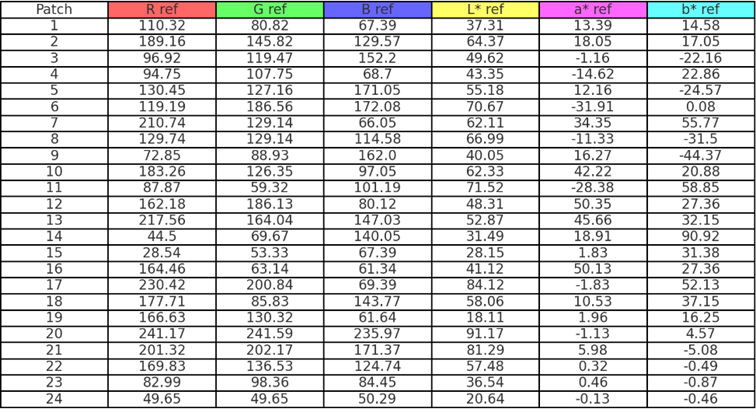
To assess the color accuracy of a camera, we commonly use a “color chart” with reference colors printed on it, such as the Xrite color chart below:

Please note that the color references have been changed after November 2014. Post-November 2014, the references are as follows:
Then, by taking a picture of this chart, it is possible to evaluate the color accuracy of the given camera using your own script or by using third-party tools such as Imatest. You can see below an example of such a measurement of my iPhone 13 under the D65 illuminant:
Ok! Well, we have a measure of the Delta E for every color patch. But what does it mean? And how is it calculated? Let me explain everything below.
Understanding Delta E
In our quest for color accuracy, Delta E emerges as a crucial metric. Developed by the International Commission on Illumination (CIE), it quantifies the difference in visual perception between two colors. The term Delta signifies change, while ‘E’ derives from the German word ‘Empfindung’, meaning sensation.
The value obtained by measuring the Delta E can be interpreted as follows:

Please note that this table is subjective and can depend based on your applications.
Delta E 1976 (dE76)
The first incarnation of the Delta E metric, dE76, uses the straightforward Euclidean distance in the CIELAB color space. The equation for this is:
\[\Delta E_{76} = \sqrt{(L_2 – L_1)^2 + (a_2 – a_1)^2 + (b_2 – b_1)^2}\]
Visualize this as measuring the direct path between two points in a three-dimensional color landscape. However, its simplicity is a double-edged sword; it does not account for the nonlinearities in human color perception, which can lead to discrepancies in color-intensive applications.
Below is an image demonstrating how dE76 calculates color difference as a simple Euclidean distance in the LAB color space:
Delta E 1994 (dE94)
As industries demanded more nuanced color differentiation, dE94 was introduced, refining the earlier model by incorporating perceptual weighting factors. This version provides a more balanced approach, particularly useful in fields like printing and manufacturing, where color consistency is critical. The equation for dE94 adjusts the basic formula with additional parameters:
\[\Delta E_{94} = \sqrt{\left(\frac{\Delta L}{k_L S_L}\right)^2 + \left(\frac{\Delta C}{k_C S_C}\right)^2 + \left(\frac{\Delta H}{k_H S_H}\right)^2}\]
where:
• $\Delta L$ is the difference in lightness.
• $\Delta C$ is the difference in chroma.
• $\Delta H$ is the difference in hue.
• $k_L$, $k_C$, $k_H$ are parametric factors that are typically set to 1.
• $S_L$, $S_C$, $S_H$ are weighting functions.
CIE94 introduced a conversion of the given Lab value into CIE LCh (Lch). The two color models differ in that Lch represents hue as an angle instead of infinite points of color. This allows us to more easily troubleshoot and perform calculations on hue.
Delta E 2000 (dE00)
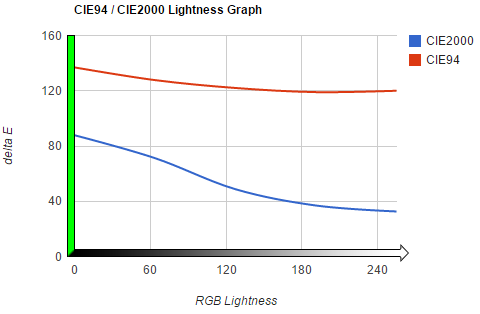
The CIEDE2000 formula, introduced in 2001, represents the most sophisticated approach to color difference measurement. It incorporates corrections for several perceptual non-uniformities, making it the most accurate for many applications. However, it also introduces complexities that require careful implementation to avoid common errors.
The formula for dE00 is:
\[\Delta E_{00} = \sqrt{\left(\frac{\Delta L{\prime}}{k_L S_L}\right)^2 + \left(\frac{\Delta C{\prime}}{k_C S_C}\right)^2 + \left(\frac{\Delta H{\prime}}{k_H S_H}\right)^2 + R_T \cdot \left(\frac{\Delta C{\prime}}{k_C S_C}\right) \cdot \left(\frac{\Delta H{\prime}}{k_H S_H}\right)}\]
where:
• $\Delta L{\prime}$ is the difference in lightness.
• $\Delta C{\prime}$ is the difference in chroma.
• $\Delta H{\prime}$ is the difference in hue.
• $S_L$, $S_C$, $S_H$ are the weighting functions for lightness, chroma, and hue, respectively.
• $k_L$, $k_C$, $k_H$ are the parametric factors (often set to 1).
• $R_T$ is a rotation term that accounts for interaction between chroma and hue differences.
The key improvements in the CIEDE2000 formula include:
1. Parametric Weighting Functions: The use of parametric weighting functions $S_L$, $S_C$, $S_H$ allows the formula to account for the non-linearities in the perception of lightness, chroma, and hue differences.
2. Rotation Term: The rotation term $R_T$ adjusts for interactions between chroma and hue differences, particularly important for colors near the blue region (around 275°).
3. Hue Adjustment: The formula includes corrections to ensure that colors differing mainly in hue are measured more accurately.
Understanding Delta C
While Delta E provides an overall measure of color difference, Delta C specifically focuses on chroma or colorfulness, which is crucial when evaluating color accuracy under varying light conditions, particularly low light. Delta C is especially useful in situations where exposure errors—variations in lightness—might distort the perception of color differences.
Exposure errors can strongly affect traditional color difference metrics like $\Delta E_{ab}$, $\Delta E_{94}$, and $\Delta E_{00}$ because they include differences in luminance (lightness). To isolate color differences from exposure errors, Delta C is used as it omits the luminance component ($\Delta L$) from the calculation, allowing for a clearer assessment of color accuracy without the confounding effects of varying light levels.
CIELAB Chroma Difference (ΔCab):
\[\Delta C_{ab} = \sqrt{(\Delta a)^2 + (\Delta b)^2} = \sqrt{(\Delta E_{ab})^2 – (\Delta L)^2}\]
This formula calculates the color difference in the ab plane, effectively removing the lightness difference ($\Delta L$), making it particularly useful in evaluating color consistency where lightness may vary, such as in low-light conditions.
CIE94 Chroma Difference (ΔC94):
\[\Delta C_{94} = \sqrt{\left(\frac{\Delta C}{S_C}\right)^2 + \left(\frac{\Delta H}{S_H}\right)^2}\]
This version adjusts the chroma and hue differences by perceptual weighting functions, further refining the color difference measurement while excluding the lightness component.
CIEDE2000 Chroma Difference (ΔC00):
\[\Delta C_{00} = \sqrt{\left(\frac{\Delta C{\prime}}{k_C S_C}\right)^2 + \left(\frac{\Delta H{\prime}}{k_H S_H}\right)^2}\]
In the CIEDE2000 standard, $\Delta C_{00}$ omits the $\left(\frac{\Delta L{\prime}}{k_L S_L}\right)^2$ term from the $\Delta E_{00}$ equation, focusing solely on chroma and hue differences.